Thinking Tools learners can do a number of things in maths that most traditionally taught learners can’t — not because they are “smarter,” but because they’ve been trained to work with the brain’s natural learning mechanisms instead of against them.

Here’s the core difference: most learners are taught how to execute procedures, while Thinking Tools learners are taught how to think before they execute.

Pattern Recognition as a Thinking Tools Skill

Why it matters:
Mathematics is built on patterns — number sequences, geometric relationships, proportional reasoning, and algebraic structures. Learners who are trained in rote procedures often overlook these because they’re too focused on “what comes next” in the method.

What Thinking Tools learners do differently:

• In Step 0, before calculating, they scan the problem for connections to something they’ve seen before.
• They ask: “Does this look like another problem I solved? What’s the same, what’s different?”
• They spot hidden structures — e.g., factor patterns in algebra, symmetry in geometry, or repetition in sequences.
• They can transfer solutions from one context to another because they see the underlying shape of the problem, not just its surface form.

Example:
A learner sees the sequence 3, 6, 12, 24, …

• Traditional learner: Might keep adding or multiplying without thinking why.
• Thinking Tools learner: Immediately recognises “each term × 2” → predicts future terms and links it to powers of two.

Advantage:
Pattern recognition speeds up problem solving, strengthens prediction skills, and allows learners to jump into unfamiliar contexts with more confidence.

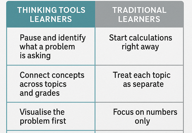
1. Start with Step 0 Instead of Step 1

• What most learners do: See a question → jump straight to calculation or memorised method.
• What Thinking Tools learners do: Pause, scan the problem, identify what it’s really asking, and decide which maths principles or laws could apply.
• Advantage: They can adapt to unfamiliar problems because they’re not locked into rote pathways.

2. Link Maths Across Topics and Grades

• What most learners do: Treat fractions, algebra, geometry, and trigonometry as separate silos.
• What Thinking Tools learners do: Break the “grade barrier” and see how one idea supports another — e.g., how ratio thinking underpins both fractions in Grade 5 and gradient in algebra later.
• Advantage: Stronger transfer skills — they can borrow a method from one branch of maths to solve a problem in another.

3. Visualise Before They Calculate

• What most learners do: Follow the numbers without creating a mental picture.
• What Thinking Tools learners do: Create a mental (or sketched) model first — shapes, number lines, fraction bars, coordinate grids.
• Advantage: They spot relationships and errors earlier, and they can explain their thinking to others.

4. Articulate Their Reasoning

• What most learners do: Get an answer but struggle to explain how.
• What Thinking Tools learners do: Use the language of thinking — “I compared… I noticed… I decided…” — so they can justify every step.
• Advantage: Stronger in oral exams, group problem solving, and peer teaching.

5. Handle “Never-Seen-Before” Problems

• What most learners do: Freeze or guess when the problem doesn’t look like a textbook example.
• What Thinking Tools learners do: Break it down into familiar components, link to known laws, and build a path from what they know to what they don’t.
• Advantage: Far greater resilience in tests, olympiads, and real-life problem solving.

6. Avoid the “Practise More” Trap

• What most learners do: Believe doing more of the same sums = improvement.
• What Thinking Tools learners do: Understand that improvement comes from refining strategies, not just repetition.
• Advantage: Faster progress with less burnout.